The law of gravity

At the time of Newton it was perfectly understood that there existed a force called ``gravity'' that made all objects fall to the ground. Newton conjectured that the same force was responsible for the Moon orbiting the Earth and the planets orbiting the Sun.

If that was indeed the case, the force acting on the Moon should be about 3600 weaker than the force causing objects to fall to the ground. Since the distance to the Moon was about 60 times the size of the Earth, the force of gravity had to obey the inverse square law:

$${1\over 3600} = {1\over 60^2}.$$

Using the inverse square law for the gravitational force, Newton was able to derive all three Kepler's law of planetary motions.

Using additional arguments, Newton finally arrived at the formula that gives the force of gravity between two objects with masses M₁ and M₂:

$$F_g = G{M_1 M_2\over R^2}$$

where R is the distance between two objects, and G is a fundamental constant, i.e. a number that is the same at all times and everywhere in the universe:

$$G = \left(6.6726\pm 0.0008\right)\times 10^{-11} {{\rm m}^3\over {\rm kg}\,{\rm s}^2}.$$

This is the worst known fundamental constant.

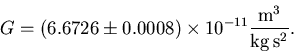
If one of the objects is much larger than the other (as, for example, the case of the Sun and a planet), then the mass of the larger object is usually denoted by M, and the mass of the smaller object is denoted by m:

$$F_g = G{m M\over R^2}.$$

We can now understand why all objects fall to the ground with the same acceleration (and, thus, in the same time if they fall from the same height). From Newton's second law:

$$m g = F_g = G{m M\over R^2}$$

(note that I use g instead of a, it is a common notation for the gravitational acceleration). Since m appears on both side, it can be canceled out:

$$g = G{M\over R^2}.$$

There is no m any more in this equation, which means that g is independent on the mass of a falling object. At the surface of the Earth

$$g = 9.8\, {\rm m}/{\rm s}^2.$$

Oops! Do we have a problem?

In the equation:

$$g = G{M\over R^2}$$

G is constant (does not change no matter what), M is the mass of the Earth (does not change no matter what), but R is the distance to the center of the Earth, and it can change. For example, when we go to the eleventh floor of the Gamow tower, we move further from the center of the Earth, and we therefore should weight less at the 11th floor than on the 1st floor.

A:

True.

B:

False.

The third Kepler's law

The third law of Kepler:

P² = R³,

(with P measured in years and R in astronomical units) can be derived from the Newton's law of gravity for any pair of objects orbiting each other, not necessarily the Sun and a planet:

$$G(M_1+M_2)P^2 = 4\pi^2 R^3.$$

What is important is that the relationship between the size of a system (in this case R) and the measure of how fast objects are moving (in this case the period P) depends on the total mass of the system. Thus, if we know the size of the gravitating system, and how fast objects inside this system are moving, we can apply an appropriately modified form of the Kepler's law to measure the total mass of the system - this is one of only two direct ways to measure masses of astronomical objects.