After the Michelson-Morley experiment, the scientists were left with two equally unpleasant alternatives:
Various explanations were immediately proposed.
Ether drag was partially supported by the fact that the speed of light in a medium is always smaller than the speed of light in vacuum. However, in that case shouldn't the Earth experience some friction, and as the result spiral down and fall to the Sun?
Both explanations were not satisfactory. Austrian physicist and philosopher Ernst Mach offered a different explanation:
The Michelson-Morley experiment was designed to detect ether. No ether was detected, therefore, there was no ether at all.
This explanation fully follow the rules of science. However, it was difficult to accept since there was no alternative theory!
Based on the FitzGerald hypothesis, Hendrik Lorentz discovered a coordinate transformation, i.e. a way of relating two different reference frames, which kept the speed of light, and thus Maxwell's equations invariant. This transformation has been called Lorentz transformation ever since.
Important note: for speeds much less than the speed of light, both transformations are identical.
However, for speeds close to the speed of light, Lorentz transformation predicted weird things: lengths should contract and time intervals should increase (time dilation). This seemed so radical, that few people were ready to accept this.
Then there came a patent examiner from Bern, named A.E.
He realized, that these weird things like length contraction and time dilation were not absolute, but relative. In other words, they only appeared.
Einstein based his theory on the relativity principle:
Einstein also believed in Maxwell's equations, and since Maxwell's equations require that the speed of light is the same in all reference frames, he simply stated that:
Thus, he accepted Lorentz transformation and discarded Galilean transformation.
In doing so, he created the Special Theory of Relativity, or SR.
![]() You book says:
You book says:
Einstein had the audacity and courage to abandon Galilean relativity completely, and with it Newtonian mechanics...
Important conclusions of SR:
Both, the length contraction, and the time dilation, are described by one
quantity, called the boost factor, or simply ![]() factor, because
it is traditionally denoted by a capital Greek letter
factor, because
it is traditionally denoted by a capital Greek letter ![]() .
.
If an object is moving with respect to a specific reference frame,
it appears that all lengths along the direction of motion
are contracted ![]() times, and all times are slowed down
times, and all times are slowed down ![]() times on this object.
times on this object.
If the speed of an object is much smaller than the speed of light, the
![]() factor is almost exactly 1, and Newtonian mechanics with
Galilean relativity rules. When the speed of an object approaches
the speed of light, the
factor is almost exactly 1, and Newtonian mechanics with
Galilean relativity rules. When the speed of an object approaches
the speed of light, the ![]() factor becomes infinitely large,
and then deviations from the Galilean relativity become very large.
factor becomes infinitely large,
and then deviations from the Galilean relativity become very large.

Since the time and the length appear differently to different observers, i.e. they become relative, it is important to have some invariant quantities as well.
Proper time is the time that is measured in the reference frame that is at rest with respect to an object.
Proper length is the length that is measured in the reference frame that is at rest with respect to an object.
Thus, if you want to measure a proper length of an object, or a proper time interval between two events, you need to be in the reference frame that is at rest with respect to this object or events.
Modern physics has shown that all fundamental forces result from the exchange of particles. Two objects feel an electromagnetic force between them because they exchange a massless particle - photon. The gravitational force appears when two objects exchange another kind of massless particles, called graviton.
They both move with the same speed - the speed of light. Hence, the speed with which the gravity force propagates is the speed of light, not infinite as predicted by the Newton's law.
The Lorentz transformation appears if there is a finite speed for any force propagation. Galilean transformation will hold in a universe where forces propagate with the infinite speed.
According to Galilean transformation, if a ball is thrown in a moving train,
an observer on the ground would measure its speed as
What if
The Lorentz transformation has a special formula for adding relativistic speeds. If you add two speeds that are less than c, you always get a speed that is less than c.
Electromagnetic radiation (light) of different kinds can be characterized
by its frequency, or a wavelength. Those two are not
unrelated. If you know the frequency (call it ![]() ), you can find out
the wavelength (call it
), you can find out
the wavelength (call it ![]() ), because
), because
The Doppler effect is the change of the light frequency (wavelength) if the light is emitted by a source moving with respect to an observer.
It is customary to measure the Doppler effect by a quantity called the
redshift, denoted by a letter z:
Why do scientists need the Doppler effect? It is a scientist's radar gun. With this effect, scientists can measure speeds of very distant objects in the universe.
(Of course, the policeman's radar gun also uses the Doppler effect to measure the speed of a passing car.)
One of the main predictions of the Einstein's SR is the rest energy.
In Newtonian mechanics, an object can have three different kinds of energy:
In SR, there is a fourth kind of energy, the rest energy.
Every object and body in the universe possesses an amount of energy
proportional to its mass:
In Newton's theory, there is no rest energy, or, more precisely, the theory does not tell anything about it.
In particle-antiparticle annihilation experiments, the SR was wonderfully confirmed!
The rest energy is enormous compared to other types of energy. The rest energy of an average person, if fully used, is enough to satisfy the energy needs of the whole world for 45 days! 1
Another important conclusion of the Einstein's theory, is that
the sum of the rest and kinetic energy of an object is simply
related to the rest energy and the boost factor ![]() :
:
Thus, in order to accelerate an object to, say, 0.9c(
![]() ), we need to spend 130% of its rest energy!
), we need to spend 130% of its rest energy!
Thus, in order to accelerate one average person to 90% of the speed of light we need to spend all the energy produced on Earth in two months!
Nuclear reactions have about 1% efficiency, i.e. mere 1% of the mass of a nuclear bomb (or nuclear reactor fuel) is converted into energy. But this is still enough to power the Sun for 10 billion years!
WARNING: the mass is the mass, it does not change when an objects moves!
Since both, space distances, and time intervals, become relative, and the
property of simultaneity is lost, we should not separate space and time any
more, but talk about space-time.
Sometimes, space-time of SR is also called Minkowski space-time,
due to Hermann Minkowski.
In space-time, an object follows a world line.
Depending on how fast objects move, their world lines can be
A major difference between usual flat (called Euclidean) space and
Minkowski space-time:
Also, the proper time along the light-like world line (a light ray)
is always zero.
Since all physical objects and signals can only move slower than or at
the speed of light, all events that can be reached from event A on
time-like or light-like world lines
form the future light cone of event A. Similarly, all
past events from which event A can be reached on time-like or light-like
world lines form the the past light cone of event A.
The principle of causality claims that only events within the past
light cone of event A could have influenced event A: looking at a distant
star is equivalent to looking backwards in time. If we look at the
Sun (never do it without dark glasses!) we see it as it was 8.3 minutes
ago.
Andy and Betty are twins. Betty rides in a spaceship at nearly the speed of
light to Alpha Centauri and back. Andy stays on Earth and waits for her return.
Who will be older when they meet?
What is some time after Betty had left, Andy jumps into a spaceship and
flies after her even faster, and eventually catches up with her.
Who will be older when they meet?
Special relativity included Newton's laws as a special case of low speeds.
However, the Newton's law of gravity is not included in SR, in particular,
according to the Newton's law, the gravitational force propagates with the
infinite speed.
Also, the distance is not absolute but relative. Which distance to use
in computing the gravity force?
We can get a clue to the ``weightlessness'' of the astronauts if we
consider an object, thrown inside the Space Shuttle (an astronaut
himself will also suffice). An object will fly in a straight line with
constant speed (until it hits a wall or someone's head). Thus, the Space
Shuttle orbiting the Earth is an inertial frame of reference!
Yes, even if the Shuttle itself does not go in a straight line!
Since it is an inertial frame, there is no force acting on a freely moving
object
If a freely falling object is an inertial frame of reference, then an object
that does not fall freely is not in the inertial (i.e. in
accelerated frame of reference.
Gravitational and inertial forces produce effects that are indistinguishable.
This is called the weak equivalence principle. It states that all
objects will move in the gravity field the same way as in the accelerated
frame of reference.
The gravity force that pulls us downward is equivalent to
upward acceleration.
Einstein went one step further, and formulated the strong
equivalence principle: all physical laws are precisely the same in
all inertial and freely falling frames, there is no experiment that
can distinguish them.
Can equivalence principles be tested experimentally? Of course yes.
The weak equivalence principle is, in fact, a result of Newton's law of
gravity. All objects fall to the ground with the same acceleration, because
the gravity force is proportional to the mass:
Thus, the weak equivalence principle states that
This was verified experimentally first by Baron Roland von Eötvös
in 1889 to the level of 1 part in 109, and then later in our century by
other to the level of 1 part in 1011.
This is fantastic accuracy! It is equivalent to noticing the size of an atom
compared to the size of our classroom!
However, equality between the inertial and gravitational masses only means
that all bodies fall with the same acceleration in the gravitational field.
It says nothing about other laws of physics. Thus, Einstein's strong
equivalence principle is not verified experimentally yet. It is, however,
supported by observations in as much as GR is supported by the data.
Three immediate conclusions:
All these conclusions have been tested experimentally.
In the presence of gravity filed, an inertial observer is not necessarily
moving in a straight line (orbiting Space Shuttle). Thus, gravity
makes straight lines curved, in other words, it changes the geometry
of space, or, more precisely (the SR is still valid!), the geometry
of space-time.
Thus, the GR is a theory of a curved (i.e. non-flat) space-time.
We are familiar with the normal, flat, Euclidean space. It is based on five
postulates, formulated by a Greek geometer Euclid:
For centuries, mathematicians tried to prove the fifth postulate. Finally,
Carl Friedrich Gauss (German) and Nickolay Lobachevsky (Russian) showed
that by changing the fifth postulate, one can create new,
non-Euclidean geometries.
Lobachevsky discovered the geometry of space with negative curvature:
Gauss discovered the geometry of space with positive curvature:
Sphere has a two-dimensional geometry with positive curvature. Such geometry is
sometimes called spherical. The geometry of space with negative curvature is
sometimes called hyperbolic geometry.
Sum of angles of a triangle is
Circumference of a sphere with radius r is
Geometry does not have to be one of the three, it can be spherical
in one region, flat in another region, and hyperbolic in even another
region.
Now we know, that
Thus, we can conclude, that
This type of world line is called a geodesic.
The scale of a given inertial frame is limited by tidal forces.
Since the gravity forces changes with distance, a force acting on one
part of an object may be different from the force acting on another
part of an object.
The tidal forces are responsible for the tides on Earth, because the
Moon gravity is different at two sides of the Earth. The water in the
ocean bulges on both sides of the Earth.
Tidal forces were responsible for the break-up of Shoemaker-Levi
comet when it fell into Jupiter.
The existence of the tidal forces means that in the gravitational field,
different places within one inertial frame feel slightly different
gravity forces, whereas in an accelerated frame all places move with
precisely the same acceleration.
Thus, the equivalence principle is not exact - it is only
approximate for any object of finite size. It becomes
exact only for a point.
It is said that inertial frames in GR are local, i.e. they
only extend for a very small distance around an observer.
After some 10 years of continuous search, Einstein finally arrived at
the equation(s) of GR (Einstein's gravity law):
Symbolically, we can write Einstein equations in the following form:
In its complete mathematical form, they look like this:
All tests of GR can be separated into two types:
weak field limit, i.e. testing GR when deviations from Newton's
gravity are weak, and
strong field limit, when deviations from the Newton's law are large.
Weak field limit test are numerous
(but they are less valuable, because
there are alternative theories of gravity):
Strong field limit tests are much more difficult to perform, but
only they can convincingly confirm (or reject!) the GR:
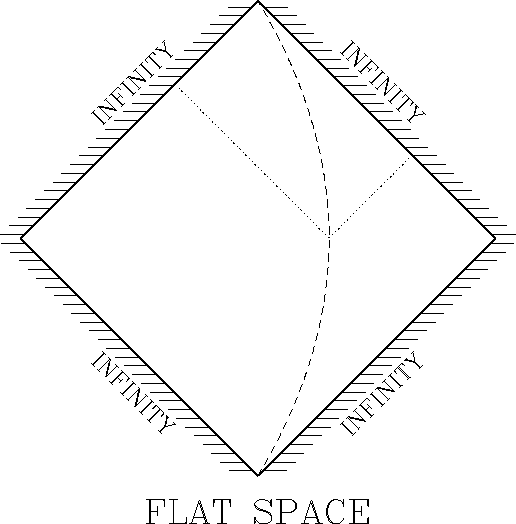
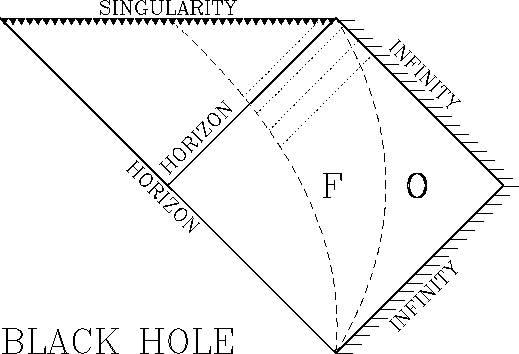
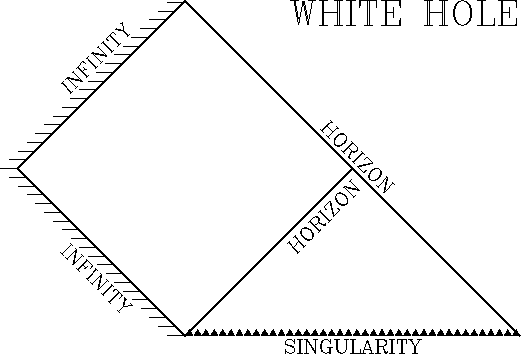
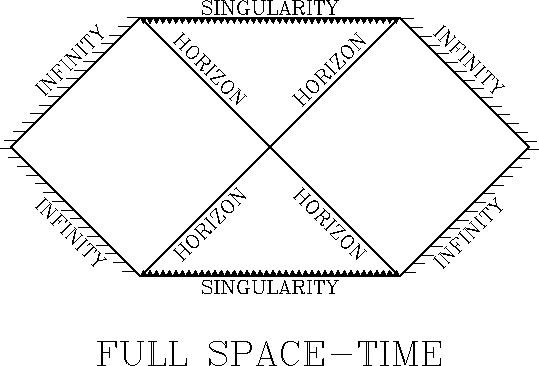
Conformal diagram is a space-time diagram, in which infinity is
(imaginary) squeezed to a finite distance from the center.
Properties of conformal diagrams:
Here are five conformal disgrams that we will use in this class:
Black holes were ``discovered'' theoretically soon after Einstein
published his GR by a German astronomer Karl Schwarzschild
(in trenches on a German-Russian front during the WWI).
A nonrotating black hole consists of a singularity (point,
where the gravitational force becomes infinite), surrounded by an
event horizon.
The singularity is space-like, i.e. nothing can avoid it.
The event horizon has a property (which is essentially its definition)
that light emitted from inside it
cannot reach any point outside it.
The ``radius'' of horizon, which is also called
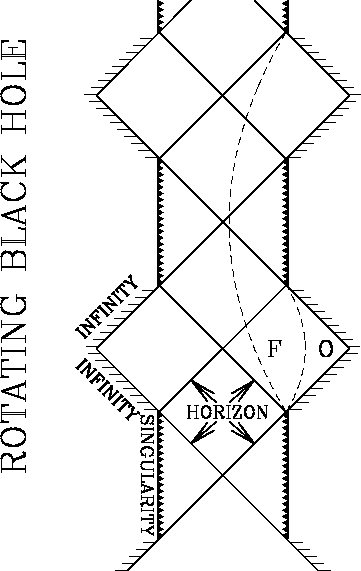
Let O be an observer well outside a black hole, and F an observer
falling into a black hole.
A rotating black hole is often called a Kerr black hole in honor
of Roy Kerr from New Zealand.
In addition to the even horizon, a Kerr black hole has an ergosphere,
a region around it where no object or light can at rest with respect
to distant stars: it has to rotate in the same direction as the black hole
itself! This is called ``dragging of inertial frames'', i.e. all inertial
frames rotate around the black hole inside the ergosphere.
In the Kerr black hole the singularity is time-like, i.e. a falling observer can bypass it and exit into a different universe
from a white hole.
Two reservations:
In GR there is a special no-hair theorem that states that isolated
black holes can be characterized only by three numbers: their mass,
their electrical charge, and their angular momentum (i.e. how fast they rotate). All other characteristics of matter which formed
a black hole are totally forgotten.
For example, if we ``construct'' two black holes with the same masses,
electrical charges, and angular momenta, but will make the first black hole
out of ordinary matter, and the second one out of anti-matter, they
would be completely indistinguishable - none of the special quantum
``charges'' (baryonic, leptonic, ``color'', ``charm'', etc) is
conserved in the black hole.
Quantum Mechanics makes a startling prediction about the black holes: if
in ordinary (so called ``classic'') mechanics noting can leave a black hole,
in Quantum Mechanics black holes can evaporate!
This process is very very slow: a black hole with the mass of the Sun will
evaporate in 1065 years! This is unimaginably slow, slower than the
thermal death of the universe.
Black holes evaporate by emitting radiation, which is called
Hawking radiation, in honor of British astrophycist Stephen
Hawking, who ``discovered'' it theoretically in 1973.
There is no direct observational proof that black holes exist. Indirect
clues:
There are two web-sites where you can experience a virtual journey into
a black hole. They both a linked to the course homepage.
``Virtual Trips to Black Holes and Neutron Stars'' by Robert Nemiroff
``Falling Into a Black Hole'' by Andrew Hamilton
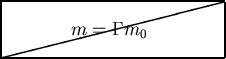
![\begin{picture}(1,0.6)(0,0)
\thicklines
\put(0.05,0.05){\framebox (0.9,0.50)[t]...
...box(0,0){electromagnetism}}
\put(0.5,0.10){\makebox(0,0){gravity}}
\end{picture}](img17.gif)
![]() On the orbit around the Earth, astronauts in the Space Shuttle feel
no gravity: they float around, move objects many times their own mass
with one finger, etc. Does it mean that there is no gravity in the outer
space?
On the orbit around the Earth, astronauts in the Space Shuttle feel
no gravity: they float around, move objects many times their own mass
with one finger, etc. Does it mean that there is no gravity in the outer
space?
![]() When the Space Shuttle lifts up, astronauts often feel several
``g'', i.e. gravity several times larger than the gravity at the
surface of the Earth. Does it mean that the gravity is stronger in
the Space Shuttle than out side it?
When the Space Shuttle lifts up, astronauts often feel several
``g'', i.e. gravity several times larger than the gravity at the
surface of the Earth. Does it mean that the gravity is stronger in
the Space Shuttle than out side it?
![]()
![]() weightlessness.
weightlessness.
![]() What is so special about the Shuttle orbiting the Earth?
What is so special about the Shuttle orbiting the Earth?
![]()
![]()
But who said that the above equation is right? We must make a distinction
between the inertial and the gravitational masses.
![]()
![]()
![]()
![]() in spherical geometry.
in spherical geometry.
![]() in flat geometry.
in flat geometry.
![]() in hyperbolic geometry.
in hyperbolic geometry.
![]() It is clear why the water bulges on the side of the Earth facing the Moon:
the Moon gravity pulls it. But why does the ocean bulge on the other
side of the Earth?
It is clear why the water bulges on the side of the Earth facing the Moon:
the Moon gravity pulls it. But why does the ocean bulge on the other
side of the Earth?
Here Gij is called the Einstein's tensor, it describes the
geometry of the space-time. Tij is called the stress-energy
tensor, it describes the matter and energy in this space-time.
![]()
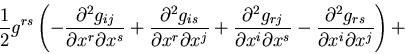
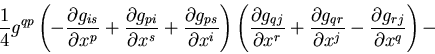
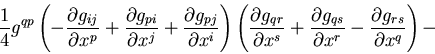
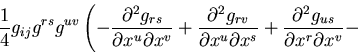
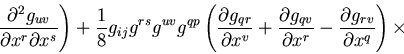
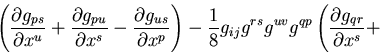
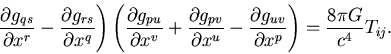
Schwarzschild
radius is proportional to the mass of the black hole.
If the Sun became a black hole (in reality it will not), its
Schwarzschild radius will be 3 km (1.8 miles).
![]() The Sun is 300,000 times more massive than the Earth. Thus, if the Earth
became the black hole, its Schwarzschild radius would be:
The Sun is 300,000 times more massive than the Earth. Thus, if the Earth
became the black hole, its Schwarzschild radius would be:
![]()
![]()
![]()
Next: About this document ...
1999-02-15