We are familiar with the normal, flat, Euclidean space. It is based on five postulates, formulated by a Greek geometer Euclid:

1.

It is possible to draw a straight line from any given point to any other point.

2.

A straight line of finite length can be extended indefinitely, still in a straight line.

3.

A circle can be described with any point as its center and any distance as its radius.

4.

All right angles are equal.

5.

Given a line and a point not on the line, only one line can be drawn through that point that will be parallel to the first line.

For centuries, mathematicians tried to prove the fifth postulate. Finally, Carl Friedrich Gauss (German) and Nickolay Lobachevsky (Russian) showed that by changing the fifth postulate, one can create new, non-Euclidean geometries.

Lobachevsky discovered the geometry of space with negative curvature:

5.

Given a line and a point not on the line, arbitrary many lines can be drawn through that point that will be parallel to the first line.

Gauss discovered the geometry of space with positive curvature:

5.

Given a line and a point not on the line, no lines can be drawn through that point that will be parallel to the first line.

Sphere has a two-dimensional geometry with positive curvature. Such geometry is sometimes called spherical. The geometry of space with negative curvature is sometimes called hyperbolic geometry.

Sum of angles of a triangle is

• greater than 180^o in spherical geometry.
• equal to 180^o in flat geometry.
• less than 180^o in hyperbolic geometry.

Circumference of a sphere with radius r is

• less than 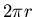$2\pi r$ in spherical geometry.
• equal to 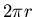$2\pi r$ in flat geometry.
• greater than 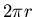$2\pi r$ in hyperbolic geometry.

• Spherical geometry is finite.
• Flat geometry is infinite.
• Hyperbolic geometry is even ``more infinite'' that the flat one.

Geometry does not have to be one of the three, it can be spherical in one region, flat in another region, and hyperbolic in even another region.