No Title

Cosmological horizon

Important feature of the Big Bang theory is the cosmological horizon. Since the universe has only a finite age, light travels only a finite distance during the age of the universe. Thus, we cannot see arbitrary far: there are galaxies in the universe that are further away than the ``light-age'' of the universe, so we cannot see them. The sphere around us with the radius equal to the ``light-age'' of the universe is called the cosmological horizon. It is about 6000 megaparsecs.

Measuring cosmological parameters

Up to now we met four cosmological parameters: H₀, q₀, $\Omega_0$ , $\Omega_\Lambda$ (q₀ is a combination of the last two, so it is not independent). There is another important parameter: the density of baryons.

Now we know that in addition to ordinary (called baryonic) matter, universe contains the so called ``dark matter''. Thus, we need to know the relative contributions of those two kinds of matter.

The density of baryons can be also expressed as an ``Omega'' parameter:

$\begin{displaymath}\Omega_B. \end{displaymath}$

Of course,

$\begin{displaymath}\Omega_B \le \Omega_0, \end{displaymath}$

and $\Omega_B=\Omega_0$ only if there is no dark matter whatsoever.

The dark matter contribution is what makes it up to the total $\Omega_0$ :

$\begin{displaymath}\Omega_X + \Omega_B = \Omega_0 \end{displaymath}$

Measuring 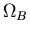$\Omega_B$

One of the best ways to measure $\Omega_B$ is to use the Big Bang nucleosynthesis. During this process, in addition to helium (⁴He), a few other isotopes are produced: deuterium, helum-3, and lithium-7 (denoted as D, ³He, and ⁷Li).

The amount of those isotopes produced depends on the density of baryons, i.e. on $\Omega_B$ . The abundances of those isotopes can be measured quite accurately, and the latest result yields:

$\begin{displaymath}\Omega_B \approx 0.04 \end{displaymath}$

(for H₀=70, since it depends on H₀ as well).

This is a rather strong confirmation of the Big Bang theory, since only one parameter - the baryon density - is used to explain four different abundances.

Another way of measuring $\Omega_B$ is offered by the CMB anisotropies.

Measuring 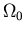$\Omega_0$

To measure $\Omega_0$ , we need the measure the amount of matter in the universe, i.e. ``weight'' the whole universe. We can measure all the matter in galaxies using the Kepler's third law: we know how large the galaxies are, and how fast they rotate. But if most of the matter in the universe is dark, how would one measure it?

Perhaps, one of the best ways to do so is to look at clusters of galaxies. Galaxies move along their orbits inside a cluster the same way the stars move in a galaxy. Thus, using the Kepler's third law we can measure masses of galaxy clusters. Then astronomers make an assumption that clusters of galaxies are representative pieces of the universe, i.e. they on average contain the same ratio of the dark matter to visible matter (stars in galaxies) as the universe in the whole.

Then one can make a proportion:

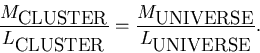
$\begin{displaymath}{M_{\mbox{CLUSTER}}\over L_{\mbox{CLUSTER}}} = {M_{\mbox{UNIVERSE}}\over L_{\mbox{UNIVERSE}}}. \end{displaymath}$

We can measure $M_{\mbox{CLUSTER}}$ , $L_{\mbox{CLUSTER}}$ , and $L_{\mbox{UNIVERSE}}$ . Thus, using the proportion we can measure the ``mass'' of the universe. (In practice, astronomers measure the density, i.e. the amount of mass in a given finite volume).

This measurement is not very accurate, and gives

$\begin{displaymath}\Omega_0 \approx 0.2. \end{displaymath}$

But it is almost certain that this assumption is incorrect, and $\Omega_0$ is somewhat larger than that.

And again, the spectrum of the CMB has a clue about $\Omega_0$ hidden in it.

Cluster gas fraction

There are many reasons to think that clusters contain more galaxies per dark matter than present on average in the universe. But at the same time there are no reasons whatsoever to assume that there same is true for the intracluater gas.

Clusters of galaxies contain intracluater gas, and the mass of this gas is usually 10 times larger than the mass of galaxies (i.e. clusters should indeed be called ``clusters of gas'' rather than ``clusters of galaxies''). Within modern physics there is no known way to enhance or diminish the fraction of this gas inside a cluster. Thus, we can safely assume that

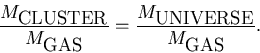
$\begin{displaymath}{M_{\mbox{CLUSTER}}\over M_{\mbox{GAS}}} = {M_{\mbox{UNIVERSE}}\over M_{\mbox{GAS}}}. \end{displaymath}$

We can measure the amount of gas in clusters because they emit X-rays.

The stumbling block: we do not know the mass of gas in the universe! (i.e. $\Omega_B$ ).

Thus, we can proceed in three different ways:

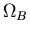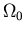If we believe that nucleosynthesis gives us the right value for $\Omega_B$ , we can use the cluster gas fraction to deduce that $\Omega_0$ = 0.04/0.1 = 0.4.
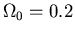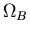If we believe that $\Omega_0=0.2$ , then we can use the cluster gas fraction to deduce that $\Omega_B$ = 0.2*0.1 = 0.02, below the value the nucleosynthesis gives.
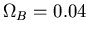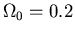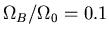We can use all three numbers, $\Omega_B=0.04$ , $\Omega_0=0.2$ , and cluster gas fraction $\Omega_B/\Omega_0=0.1$ to come up with the inconsistency:

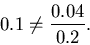
$\begin{displaymath}0.1 \neq {0.04\over 0.2}. \end{displaymath}$

The preferred way out of this incocnsistency is to think that $\Omega_0$ is somewhat larger than what is measured in clusters, perhaps 0.4 rather than 0.2.

Measuring q₀

Up to very recently, it was practically impossible to measure q₀ directly due to the lack of good standard candles. Only in 1995 there was a new set of good standard candles found: supernovae Ia. As with Cepheids, they are not standard candles per se, i.e. not all supernovae Ia are of the same luminosity.

With Cepheids, their luminosity can be determined from their period.
With SN Ia, their luminosity can be determined from how fast they dim after the explosion.

Supernovae Ia are much much brighter than Cepheids, so with them one can measure distance up to almost the horizon.

The most recent results from this observational program gives

$\begin{displaymath}q_0 \approx -0.4. \end{displaymath}$

This result has immediate consequence:

We live in a universe with the cosmological constant!

Knowing a value of q₀ and that the universe if flat, we can find $\Omega_0$ and $\Omega_\Lambda$ :

$\begin{displaymath}\Omega_0 = 0.4\ \ \ \mbox{and}\ \ \ \Omega_\Lambda=0.6. \end{displaymath}$

These numbers are not very accurate, so the combination

$\begin{displaymath}\Omega_0 = 0.3\ \ \ \mbox{and}\ \ \ \Omega_\Lambda=0.7. \end{displaymath}$

is also consistent with existing observations.