Mixed Topics with the Pencil Code

MRI in 1-D

Determine the growth rate for various values of the B field.

Study the effects of viscosity and resistivity.

MRI in 2-D

Watch the streaming instability.

How large does the velocity get?

Magneto-buoyancy in an isothermal layer

Watch the rise of the tube with ".r pvid.pro"

Try different initial amplitudes

Try different initial positions

What do you get in 3-D?

AlfvenWave_SIunits

Mean-Field Dynamos

Mean-Field Spherical and Lambda Effect

→ Description: ForceFree.html.
→ Working material: ForceFree/, ForceFree.tar.gz [untar this file by typing tar zxf MeanFieldSpherical.tar.gz]

→ Description: LambdaEffect.html.
→ Working material: LambdaEffect/, LambdaEffect.tar.gz [untar this file by typing tar zxf LambdaEffect.tar.gz]

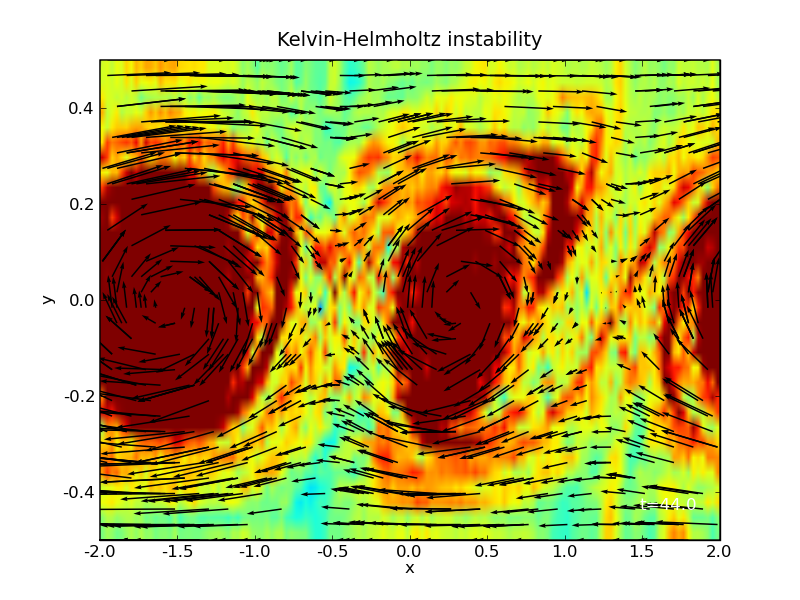
Kelvin-Helmholtz Instability

&hydro_init_pars
  inituu='tanhy', 'gaussian-noise'
  ampluu=.15, .05
  widthuu=.05
/

Parker Wind

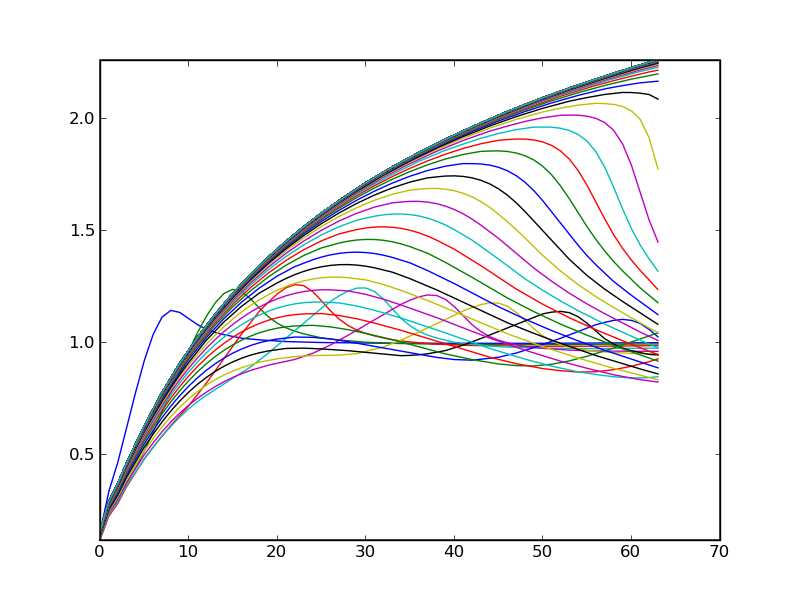
The isothermal Parker wind is a solution of the equations

u du/dr = -cs^2 dlnrho/dr - GM/r^2 and
d(r^2 rho ur)/dr = 0

There is a critical point at r=GM/2cs^2. The numerical solution approaches the wind after some equilibration process. The inital condition was just ur=1.

Bondi Accretion

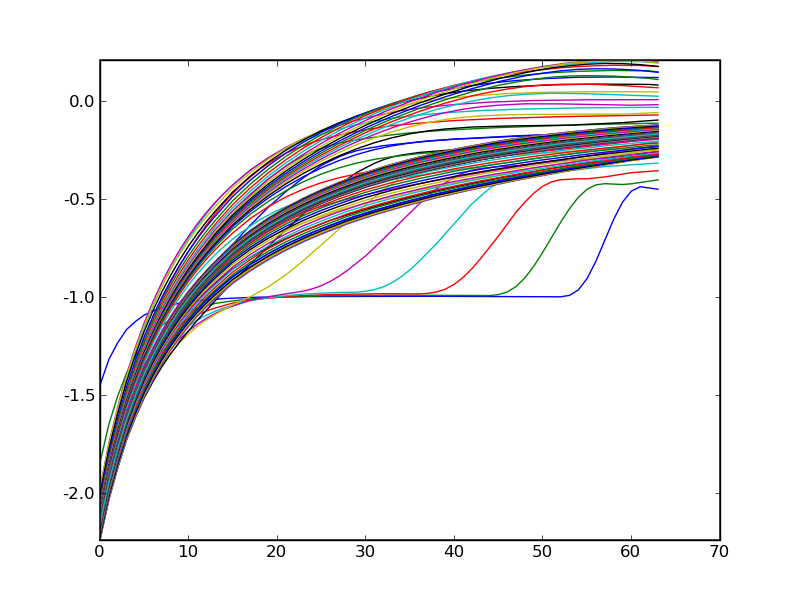
This picture on the right shows the evolution of the radial velocity at different times. The initial condition was ur=-1. As time goes on, the code approaches an equilibrium solution that corresponds to the solution of Bondi describing radial accretion.

Convection with radiation & ionization

cvs co KramersConv_Ionization

Tayler Instability

cvs co public_html/teach/PencilCode/material/TaylerInstability