Nonlinear sound waves
→ Working material: NonlinearSound/,
NonlinearSound.tar.gz
[untar this file by typing tar zxf NonlinearSound.tar.gz]
In this nonlinear sound wave problem we solve the fully compressible
equations in one dimension.
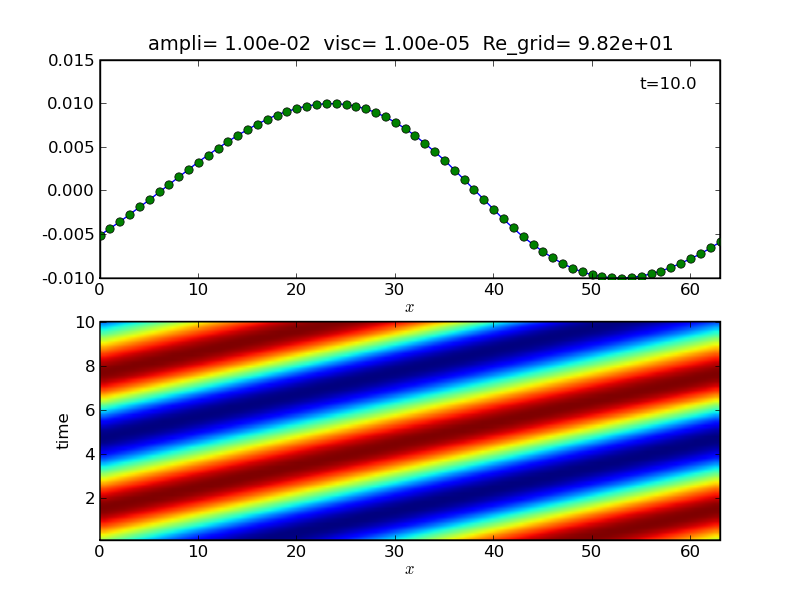
For a weak initial amplitude you find regular sound waves.
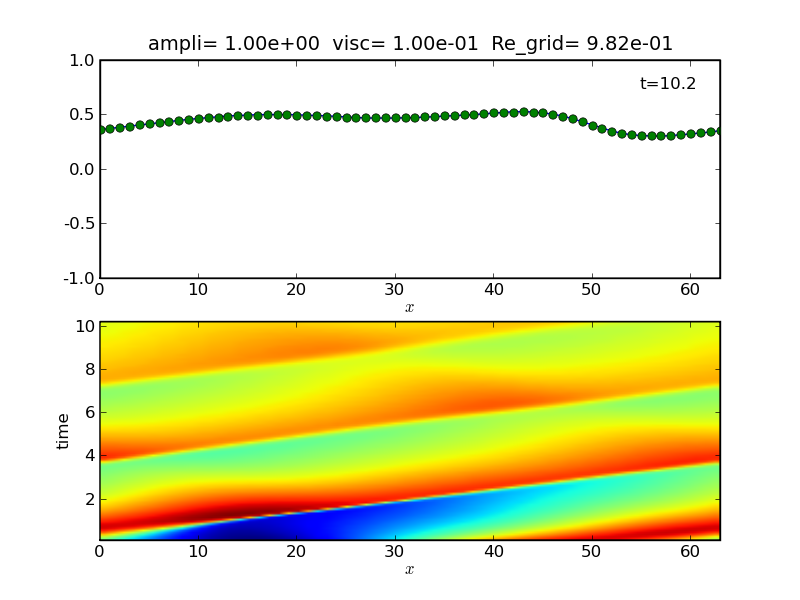
As the amplitude is increased, the initial kinetic energy
becomes comparable with the thermal energy.
Obviously, viscosity is required to prevent wiggles.
However, this leads to a decrease in amplitude and hence
a loss of kinetic energy.
Since total energy is conserved, this must lead to corresponding
heating.
Verify that total energy is indeed conserved,
and find cases where this is not the case.
What went wrong in those cases?
| Linear case A=1e-2 |
 |
| Nonlinear case A=1 |
 |
Numerical Experiments homepage
$Date: 2009/04/23 13:49:00 $, $Author: dintrans $, $Revision: 1.4 $



