Convection in the upper parts of stars
A snapshot of the temperature structure in the sun.
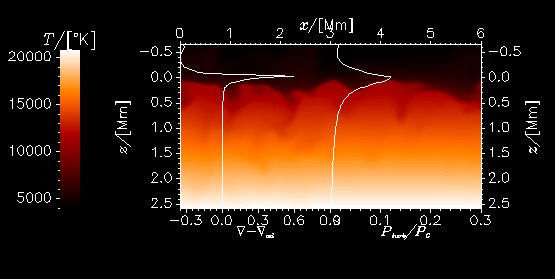
The image depicts a vertical slice in the box where downward is
inward to the center of the sun. The graph to the left shows the
superadiabatic gradient, whereas the other graph shows the
turbulent- to total-pressure. Both quantities are nonzero only
in a very thin layer in the photosphere. These two qauntities
also reveals the main problems with the Mixing Length Theory
(MLT), which cannot produce a superadiabatic layer without some
fudging, and which don't consider turbulent pressure at all.
The temperature fluctuations in the sun.
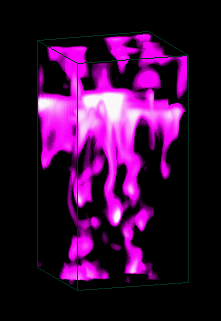
Here I show only temperatures cooler than the mean, to clearify
the picture of cool downdrafts. This picture covers the whole
depth of the simulation but only a quarter of the horisontal
extend, hereby containing a little more than one convection cell
(granule). One gets the impression of cool downdrafts that plunge
downwards, and the head of these features gets compressed as it
rams into the surrounding gas.
Abstract:
I simulate the convection in the uppermost layers of stars, by
means of a program, written by Åke Nordlund and Bob Stein.
This program incoorporates a realistic equation of state,
realistic opacities including absorption from a wide range of
molecules and a sophisticated treatment of 3D radiative transfer.
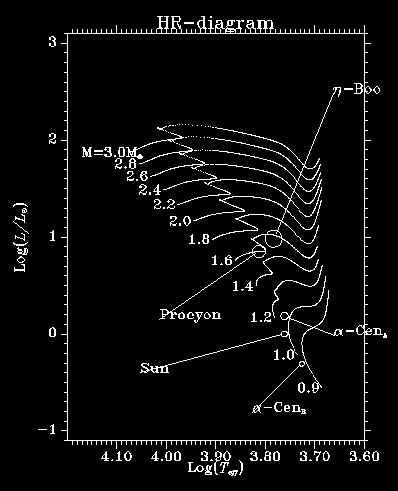
I have, by now, made simulations of 5 different stars; The Sun,
eta-Booti, alpha-Cen A and B and Procyon, and from these
simulations I hope to get able to make a simplified model of
convection that works for a wide range of stars, and is suitable
for inclusion in stellar evolution codes.
The model:
The calculations are performed on a 100x100x82 grid, with 20% of
the box being above T=Teff (the photosphere) and the rest of the
box being large enough to cover the superadiabatic region and
the region where the turbulent pressure is significant. In the
Sun this means about 13 pressure scale heights, ranging from
optical depths; Logtau=[-2,8].
The boundaries in the horisontal (x/y) directions, are periodic
and derivatives are found by fourier transforms, whereas in the
vertical, z-direction, the boundaries are open and penetrateable,
and we use spline derivatives. The bottom boundary is moved up
and down, to obtain a zero nett massflux and there is a node in
any excited p-mode at the bottom of the box.
Some results:
Some day I'll put some graphs here.
Back to the main page or back to the
convection page.
Last updated
[an error occurred while processing this directive]



